二分查找 & 二分答案
大约 8 分钟
二分查找-java算法模版
零、二分查找 & 二分答案算法全景图
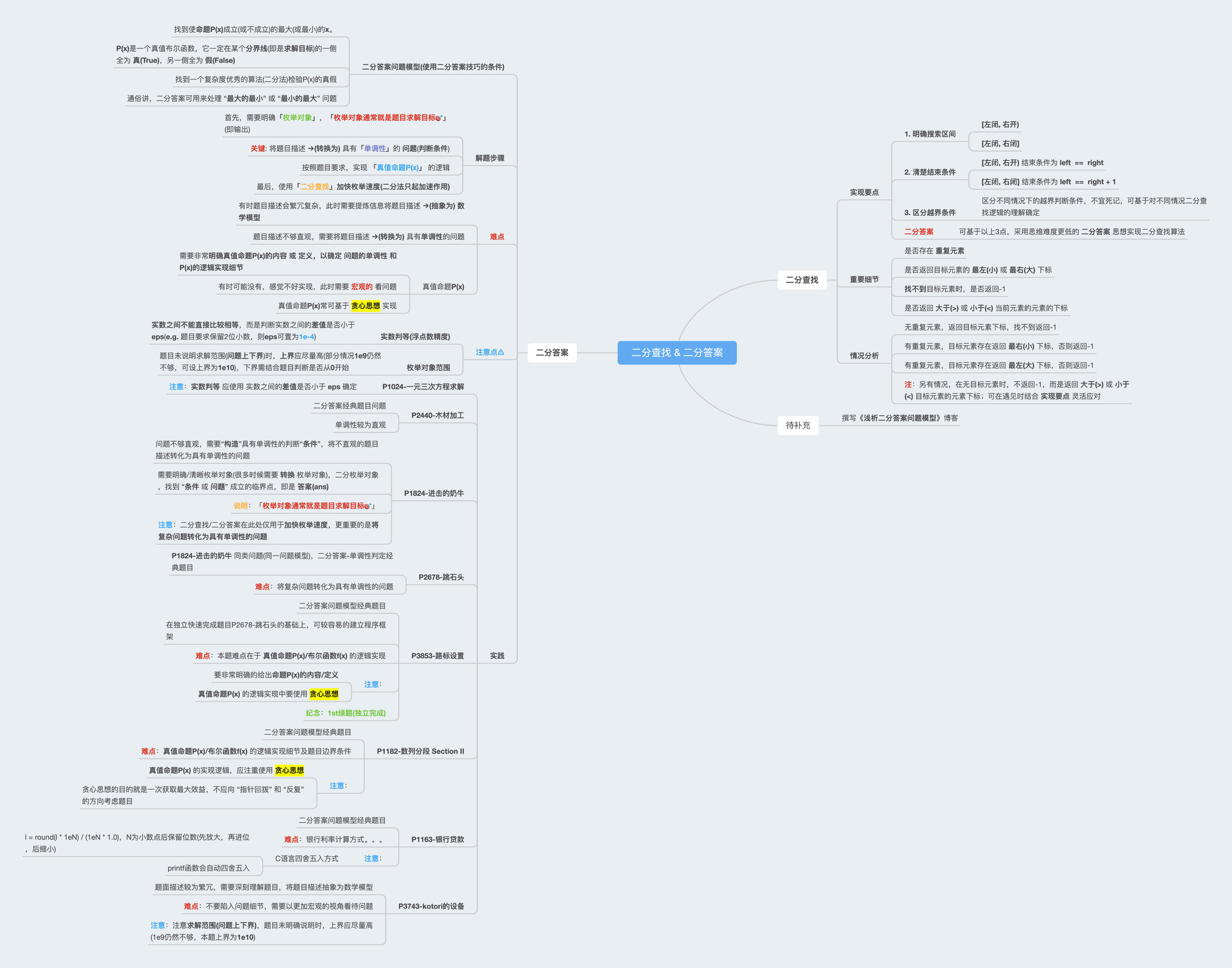
一、二分查找-算法模版
// 二分查找标准模版
// 二分查找主要有以下3种实现方式
// 1. [左闭, 右开)
// 2. [左闭, 右闭]
// 3. 二分答案写法
/**
* 二分查找要点
* 1. 明确搜索区间
* 1.1 [左闭, 右开)
* 1.2 [左闭, 右闭]
* 2. 清楚结束条件
* 搜索区间决定结束条件
* [左闭, 右开) 结束条件为 left == right
* [左闭, 右闭] 结束条件为 left == right + 1
* 3. 区分越界条件
* 区分不同情况下的越界判断条件,不宜死记,可基于对不同情况二分查找逻辑的理解确定
* 在融汇以上3点的情况下,可写出不同情况下的二分查找算法,也可基于思维难度更低的 二分答案 思想实现算法
* @author RaySunWHUT
* @Date 2023-07-12 09:37
*/
public class Main {
/**
* 搜索区间: [左闭, 右闭]
* 返回目标元素 target 最小(左)下标(第一次出现位置)
* @param arr
* @param target
* @return
*/
public int findLeftClosed(int[] arr, int target) {
// 1. 搜索区间: [left, right]
int left = 0;
int right = arr.length - 1;
// 2. 结束条件: left = right + 1
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] > target) { // 在 mid 的左侧区间 [left, mid - 1] 搜素
right = mid - 1;
} else if (arr[mid] < target) { // 在 mid 的右侧区间 [mid + 1, right] 搜素
left = mid + 1;
} else if (arr[mid] == target) { // 为清晰逻辑, 等于(==)目标元素时的分支也要写清楚
right = mid - 1;
}
}
// 左右均会越界, 关键看返回什么
// 2种越界情况:
// 1. 目标元素 大于(>) 元素序列的所有元素时(left == arr.length, right == arr.length - 1), 返回 -1
// 2. 目标元素 小于(<) 元素序列的所有元素时(left == 0, right == -1), 返回 -1
// 为提高程序健壮性 和 方便记忆, 最好写成 if (left >= arr.length || right < 0), 此处是为了清晰程序的可达性
if (left >= arr.length) {
return -1;
}
// 目标元素存在时, 返回元素最小(左)下标; 目标元素不存在时, 返回 大于(>) 目标元素的元素的最小(左)下标
// 注: 由于 left = right + 1, 故也可返回 right + 1
// return left;
// 目标元素存在时, 返回元素最小(左)下标; 目标元素不存在时, 返回 -1
// 此处, left 可替换为 right + 1
return arr[left] == target ? left : -1;
}
/**
* 搜索区间: [左闭, 右闭]
* 返回目标元素 target 最大(右)下标(最后一次出现位置)
* @param arr
* @param target
* @return
*/
public int findRightClosed(int[] arr, int target) {
// 1. 搜索区间: [left, right]
int left = 0;
int right = arr.length - 1;
// 2. 结束条件: left = right + 1
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] > target) { // 在 mid 的左侧区间 [left, mid - 1] 搜素
right = mid - 1;
} else if (arr[mid] < target) { // 在 mid 的右侧区间 [mid + 1, right] 搜素
left = mid + 1;
} else if (arr[mid] == target) {
left = mid + 1;
}
}
// 左右均会越界, 关键看返回什么
// 2种越界情况:
// 1. 目标元素 大于(>) 元素序列的所有元素时(left == arr.length, right == arr.length - 1), 返回 -1
// 2. 目标元素 小于(<) 元素序列的所有元素时(left == 0, right == -1), 返回 -1
// 为提高程序健壮性 和 方便记忆, 最好写成 if (left >= arr.length || right < 0), 此处是为了清晰程序的可达性
if (right < 0) {
return -1;
}
// 目标元素存在时, 返回元素最大(右)下标; 目标元素不存在时, 返回 小于(<) 目标元素的元素的最大(右)下标
// 注: 由于 left = right + 1, 故也可返回 left - 1
// return right;
// 目标元素存在时, 返回元素最大(右)下标; 目标元素不存在时, 返回 -1
// 此处, right 可替换为 left - 1
return arr[right] == target ? right : -1;
}
/**
* 搜索区间: [左闭, 右开)
* 返回目标元素最小(左)下标(第一次出现位置)
* @param arr
* @param target
* @return
*/
public int findLeftOpen(int[] arr, int target) {
// 1. 搜索区间: [left, right)
int left = 0;
int right = arr.length;
// 2. 结束条件: left == right, 此时搜索区间为[left, left), 可正确终止
while (left < right) {
int mid = left + (right - left) / 2;
if (arr[mid] > target) { // 在 mid 的右侧区间 [mid + 1, right) 搜索
right = mid;
} else if (arr[mid] < target) { // 在 mid 的左侧区间 [left, mid) 搜素
left = mid + 1;
} else if (arr[mid] == target) {
right = mid;
}
}
// 返回left时, 只有右边界会越界
// 1种越界情况:
// 1. 目标元素 大于(>) 元素序列的所有元素时(left == right == arr.length), 返回 -1
// 由于结束条件是left == right, 故此处left可替换为right
// 两种不同写法的理解:
// 此处写成 left >= arr.length, 含义是left逐渐逼近元素序列右边界, 直至与right相等
// 此处写成 right >= arr.length, 含义是right始终保持不动, left逐渐逼近, 直至两者相等
if (left >= arr.length) {
return -1;
}
// 目标元素存在时, 返回元素小(左)下标; 目标元素不存在时, 返回 大于(>) 目标元素的元素的最小(左)下标
// 注: 由于 left == right, 故也可返回 right
// return left;
// 目标元素存在时, 返回元素最小(左)下标; 目标元素不存在时, 返回 -1
return arr[left] == target ? left : -1;
}
/**
* 搜索区间: [左闭, 右开)
* 返回目标元素最大(右)下标(最后一次出现位置)
* 注意⚠️: 搜索区间[左闭, 右开)的情况下, 返回值较为特殊, 需特别记忆!
* @param arr
* @param target
* @return
*/
public int findRightOpen(int[] arr, int target) {
// 1. 搜索区间: [left, right)
int left = 0;
int right = arr.length;
// 2. 结束条件: left == right, 此时搜索区间为[left, left), 可正确终止
while (left < right) {
int mid = left + (right - left) / 2;
if (arr[mid] > target) { // 在 mid 的左侧区间 [left, mid) 搜素
right = mid;
} else if (arr[mid] < target) { // 在 mid 的左侧区间 [mid + 1, right) 搜素
left = mid + 1;
} else if (arr[mid] == target) {
left = mid + 1;
}
}
// 返回left - 1时, 只有左边界会越界(此处需特别注意⚠️: 由于 arr[mid] == target 时, left = mid + 1, 所以满足条件的 mid = left - 1, 故需要返回 left - 1)
// 1种越界情况:
// 1. 目标元素 小于(<) 元素序列的所有元素时(left == right == 0), 返回 -1
// 虽然会出现 left == right == arr.length 的情况, 但此处返回 left - 1, 所以不会触发越界情况
// 虽然结束条件是left == right, 但此处返回 left - 1 更具逻辑性
if (left - 1 < 0) {
return -1;
}
// 目标元素存在时, 返回元素最大(右)下标; 目标元素不存在时, 返回 小于(<) 目标元素的元素的最大(右)下标
// 注: 由于 left == right, 故也可返回 right - 1
// return left - 1;
// 目标元素存在时, 返回元素最大(右)下标; 目标元素不存在时, 返回 -1
return arr[left - 1] == target ? left - 1 : -1;
}
/**
* 具备 "单调性" 的真值命题P(x)
* @param arr
* @param target
* @param mid
* @return
*/
private boolean f(int[] arr, int target, int mid) {
return arr[mid] >= target;
}
/**
* 二分答案思想实现二分查找(关键在于思想)
* 注意⚠️: 可通过修改 "真值命题P(x)" 的方法逻辑以及 "分界点" 两侧的处理逻辑, 适配不同搜索区间的不同情况
* 使用二分答案写法思维难度更低,此处只举例说明 "搜索区间 为 [左闭, 右开) 查找目标元素左边界" 的情况,其他情况同理
* e.g.
* 搜索区间: [左闭, 右开)
* 返回目标元素最大(右)下标(最后一次出现位置)
* @param arr
* @param target
* @return
*/
public int findLeftOpenAns(int[] arr, int target) {
int left = 0;
int right = arr.length;
int ans = -1;
while (left < right) {
int mid = left + (right - left) / 2;
if (f(arr, target, mid)) {
// 二分答案思想
ans = mid;
right = mid;
} else {
left = mid + 1;
}
}
// 返回left时, 只有右边界会越界
// 1种越界情况:
// 1. 目标元素 大于(>) 元素序列的所有元素时(left == right == arr.length), 返回 -1
// 由于结束条件是left == right, 故此处left可替换为right
// 两种不同写法的理解:
// 此处写成 left >= arr.length, 含义是left逐渐逼近元素序列右边界, 直至与right相等
// 此处写成 right >= arr.length, 含义是right始终保持不动, left逐渐逼近, 直至两者相等
if (left >= arr.length) {
return -1;
}
// 目标元素存在时, 返回元素小(左)下标; 目标元素不存在时, 返回 大于(>) 目标元素的元素的最小(左)下标
// return ans;
// 目标元素存在时, 返回元素最小(左)下标; 目标元素不存在时, 返回 -1
return arr[ans] == target ? ans : -1;
}
public static void main(String[] args) {
// int[] arr = new int[]{1, 2, 2, 4, 7, 9, 9, 9, 13};
int[] arr = new int[]{2, 2, 4, 7, 9, 9, 9, 13};
// int[] arr = new int[]{1, 2, 2, 4, 7, 9, 9, 9};
Main binarySearch = new Main();
int[] targets = new int[]{0, 2, 4, 9, 13, 20};
System.out.println("=== 寻找目标元素左边界 ===");
// 寻找目标元素左边界
for (int target : targets) {
int idx = binarySearch.findLeftClosed(arr, target);
System.out.println("idx: " + idx);
}
for (int target : targets) {
int idx = binarySearch.findLeftOpen(arr, target);
System.out.println("idx: " + idx);
}
for (int target : targets) {
int idx = binarySearch.findLeftOpenAns(arr, target);
System.out.println("idx: " + idx);
}
System.out.println("=== 寻找目标元素右边界 ===");
// 寻找目标元素左边界
for (int target : targets) {
int idx = binarySearch.findRightClosed(arr, target);
System.out.println("idx: " + idx);
}
for (int target : targets) {
int idx = binarySearch.findRightOpen(arr, target);
System.out.println("idx: " + idx);
}
}
}
注:有空可补充 灵山府二分文章